Measure of the maximum power of a supply transformer

Figura 1: Some transformers for electronic devices with different dimensions, outputs and shapes.

Transformers are common components found in many electronic devices. Up a few years ago they were the heart of the power supply of almost every low voltage device, while in the last years they've been replaced by the switching power supplies, which, for the same provided power, are lighter and more compact. While the measurement of a transformer output voltage is a simple task, an estimation of its maximum power is a complex operation. There are various criteria, more or less precise:

The size of the transformer, strongly dependent on the worker experience;
The weight, converted through coefficients;
Formulas keepin in account shape, core size, the number of windings, the cable section.

1 - The measure principle

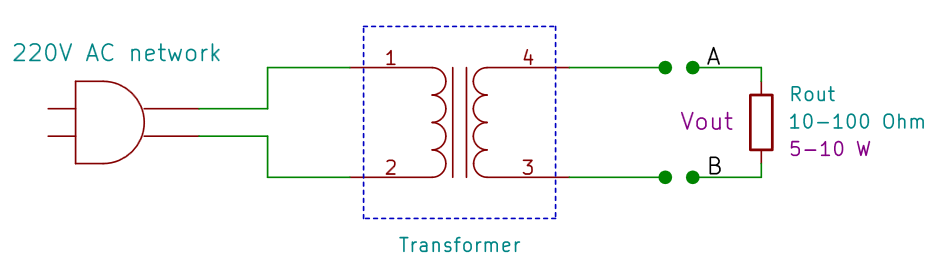
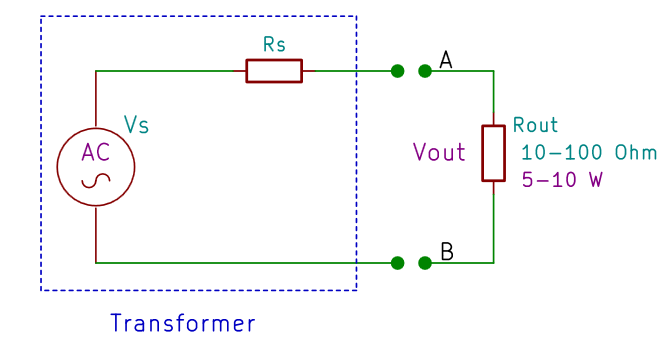
In contrast with all these methods, the procedure presented in this article is based on the measure of the transformer output voltage while it's turned on, with or without load. The main advantage is to measure directly the electrical quantities directly involved in the determination of the output power, allowing thus to obtain a good precision.

The basic idea is the following: the transformer is supplying the maximum power when its output voltage, loaded, is between the 80% and the 90% of its no-load voltage. The exact percentage n is an empirical parameter, and changes according to models, but it's anyway possible to obtain good results.

2 - The measurements procedure

Figura 2: The connection diagram for the measurement of the transformer.

To perform the measurement, this material is required:

The transformer to be measured;
A multimeter allowing to measure alternated currents (almost all models allow this);
A resistor with a value between 10 Ω and 100 &Omega, with high power (5 W or more, according to the transformer);
A plug in order to connect the transformer to the power grid.

The measurement procedure is very simple:

Measure the no-load voltage V_s(in this case it's equal to V_out);
Connect the load resistor to the transformer output (please remember it must have low resistance values, between 10 Ω e i 100 &Omega, and a high power, 5 W or more);
Measure the output voltage V_out at the resistor (that is, between A and B);
Compute the transformer power as: 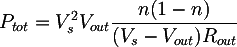$Latex: P_{tot} = V^2_s V_{out} \frac{n(1-n)}{(V_s - V_{out})R_{out}}$ where:
- V_s is the no-load voltage at the transformer output;
- V_out is the voltage at the resistor;
- R_out is the value of the resistor;
- n is an empirical value comprised between 0.8 and 0.9, typically 0.85.

It is possible to repeat the measure with many load resistors, in order to be able to plot the current-voltage plot to verify the precision of the measurement.

3 - The load resistor

The choice of the load resistor is important for the measurement. In theory, every value can be used. In practice, due to the limited multimeter resolution, it's better to choose a low resistance, for example 10 Ω or 100 Ω, in order to produce a high voltage drop at the transformer output. In this way the measure uncertainties are reduced.

Moreover, since it will have to dissipate a lot of heat, it's better to use a high power resistor, for example 5W or more, according to the transformer; the value can be computed as: 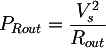$Latex: P_{Rout}= \frac{V_{s}^2}{R_{out}}$ where

P_Rout is the power of the resistor;
V_s is the no-load transformer output voltage;
R_out is the test resistor;

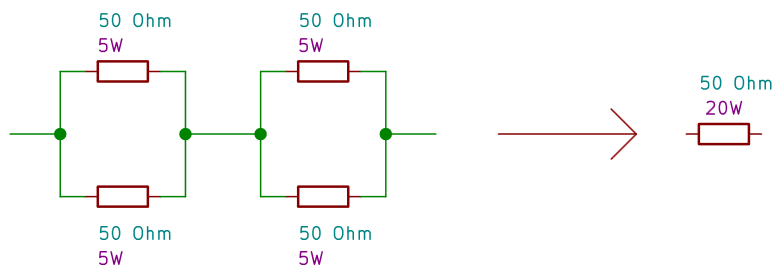
In practical situations, resistors with lower powers can be used, provided that they are connected only for a few seconds; being indeed undersized, their overheating causes first a shift in their resistance value, and then their breaking. If adequate power resistors are missing, series or parallel resistors can be used, in order to distribute the total power. An example is shown in Figura 3.

Series and parallel resistors to obtain more power

Figura 3: A possible configuration to combine resistors with the same values in series and parallel in order to obtain an equivalent circuit with the same resistance but higher dissipated power.

4 - The current - voltage plot

Once the voltage on the load R_out has been measured, it's possible to compute the supplied current with the Ohm law. If more measurements with various R_out values are performed, a voltage-current curve can be plotted, in order to verify the precision of the measurement. In case of a correct estimation, the plot is a line, which confirms the transformer ohmic behaviour when it is not supplying too much power. If the load resistor R_out is too small, that is if the power supplied by the transformer is very high, various physical phenomena would take place, such as the core saturation, which would make the transformer behaviour no longer linear; this would result in a voltage-current curve no longer straight. Moreover, in case there's an error in the measurement (wrong R_out or V_out values) the curve helps to find it.

5 - Example: transformer 1

The considered transformer has the following dimensions:

Output type: alternated current
Rated voltage: 12 V
No-load measured voltage: 14,2 V
Rated power:20 VA

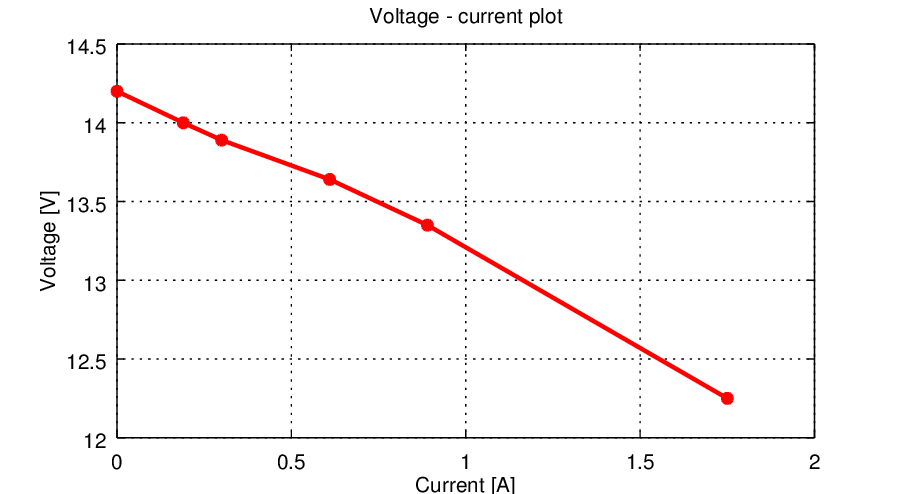
The Tabella 1 shows various measurements performed on the transformer with various load resistors. Only one would be enough to compute the maximum power with the Formula 1, but in this way it's possible to plot the graph in Figura 5 to test that the transformer has basically an ohmic behaviour. From the values obtained in the table it's possible to determine that the best estimation is for n=0.9, that is when the output voltage is the 90% of the no-load one.

Figura 4: The transformer 1 used in this example

Tabella 1: Transformer 1
Load voltage V_out	Load resistor R_out	Load current I_out	Power for n=0.9 [W]	Power for n=0.8 [W]	Internar resistance R_S
14,2	∞	0
14	73,7	0,19	17,24	30,64	1,05
13,89	46,1	0,30	17,64	31,36	1,03
13,64	22,4	0,61	19,73	35,08	0,92
13,35	15	0,89	19,00	33,78	0,96
12,25	7	1,75	16,29	28,95	1,11
Average:			18	32	1,04

Figura 5: The transformer voltage-current plot, obtained through multiple measures with different load resistors. It's a straight line, and this confirms the linear behaviour, that is ohmic behaviour, of the transformer.

6 - Example: transformer 2

The second example transformer has the following properties:

Output type: alternate current
Rated voltage: 14 V
No-load measured voltage: 15,58 V
Rated power: 24 VA

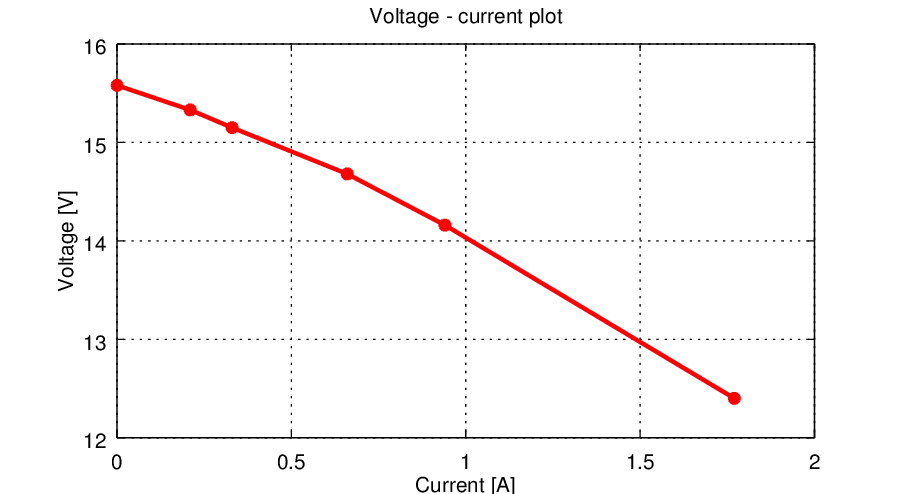
As in case of the first example, the Tabella 2 resumes the measurement results, plotted in the graph of Figura 5. In this case the best estimation is for a factor n=0.8, that is where the output voltage is the 80% of the no-load one.

Figura 6: The transformer 2 used in this example.

Tabella 2: transformer 2
Load voltage V_out	Load resistor R_out	Load current I_out	Power for n=0.9 [W]	Power for n=0.8 [W]	Internal resistance R_S
15,58	∞	0
15,33	73,7	0,21	18,18	32,31	1,20
15,15	46,1	0,33	16,70	29,68	1,31
14,68	22,4	0,66	15,91	28,28	1,37
14,16	15	0,94	14,52	25,82	1,50
12,4	7	1,77	12,17	21,63	1,80
Average:			15	27	1,43

Figura 7: As in case of transformer 1, the voltage - current plot confirms the linear and ohmic behaviour of this device.

7 - The theory

In this section the origin of the formula used to compute the maximum transformer power is shown. There are many equivalent circuits for a transformer output port; among the most simple ones, the one that simplifies it to common generator with a series internal resistor, as shown in Figura 8.

Figura 8: The transformer Thevenin equivalent circuit.

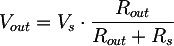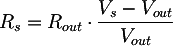
If we connect a resistor R_out at the transformer output, we obtain a voltage divider. The output voltage is: $Latex: V_{out} = V_{s} \cdot \frac{R_{out}}{R_{out} + R_{s}}$ from which we can compute the internal resistance as: $Latex: R_{s} = R_{out} \cdot \frac{V_{s}-V_{out}}{V_{out}}$

Please remember that the maximum power supplied by the transformer is when its output voltage is between 80% and 90% of its no-load voltage. Defining the parameter n, comprised between 0.8 and 0.9, the output voltage V_{out n}, corresponding to the maximum output power, is: $Latex: P_{out} = P_{tot} \rightarrow V_{out n} = n V_{s}$ We can therefore find the value of the resistor R_outn that, connected to the transformer, allow us to obtain the voltage V_outn for the maximum power; that is, we are going to compute the load to be connected to the transformer to drain from it the maximum power. 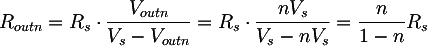From the previously computed voltage divider we obtain: $Latex: R_{out n} = R_{s} \cdot \frac{V_{out n}}{V_{s}-V_{out n}} = R_{s} \cdot \frac{nV_{s}} {V_{s}-nV_{s}} = \frac{n}{1-n}R_{s}$ The power with V_{out n} and R_{out n} is therefore: 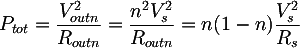$Latex: P_{tot} = \frac{V^2_{out n}}{R_{out n}} = \frac{n^2 V^2_{s}}{R_{out n}} = n(1-n) \frac{V_{s}^{2}}{R_{s}}$ From which, substituting the expression of R_s found before, we can obtain the final formula: $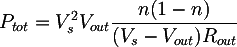Latex: P_{tot} = V^2_s V_{out} \frac{n(1-n)}{(V_s - V_{out})R_{out}}$

Tag