Categorie

Filtro passa basso attivo per subwoofer

Figura 1: Il circuto stampato del filtro passa basso attivo per subwoofer.

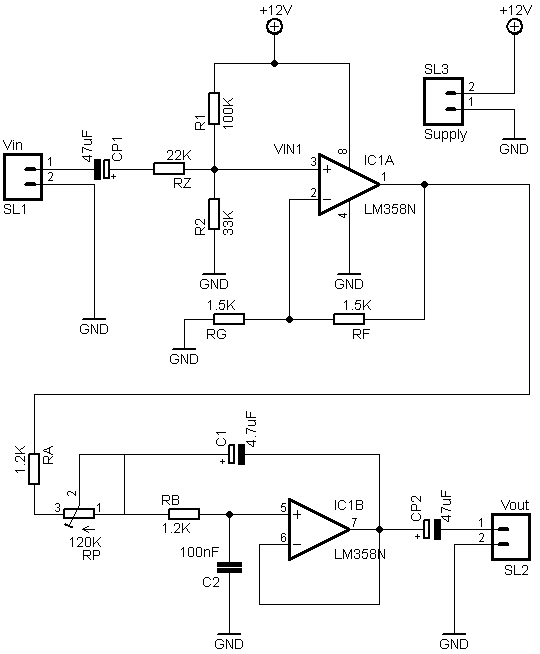
In questo articolo viene descritto un semplice filtro passa basso attivo del secondo ordine con frequenza di taglio regolabile tra 20 Hz e 200 Hz. Il circuito, che utilizza un'alimentazione singola, lavora su segnali audio di bassa potenza (livelli di linea) ed è stato pensato come elemento filtrante prima di un amplificatore collegato a un subwoofer. Il progetto è basato sulla tradizionale Cella Sallen-Key, che offre semplicità di calcolo e realizzazione a discapito di un fattore di qualità non elevato. Un'alternativa più rapida a questo circuito è il Filtro passa basso passivo per subwoofer.

1 - Caratteristiche del circuito

Figura 2: Circuito del filtro passa basso

Il comportamento del filtro è stato verificato sia mediante una simulazione con LTSpice che mediante una misura grossolana con una scheda audio del PC e il software Visual Analyser. Di seguito sono riportati i moduli delle funzioni di trasferimento del filtro nel caso di potenzionmetro impostato sulla frequenza di taglio minima (Figura 3), e massima (Figura 4). Si può notare come le due curve siano sostanzialmente coincidenti, salvo alle alte frequenze, dove la scarsa sensibilità della scheda audio e la sua rumorosità non permettono una misura precisa. La pendenza resta sempre di -40dB / decade, grazie al secondo ordine del filtro.

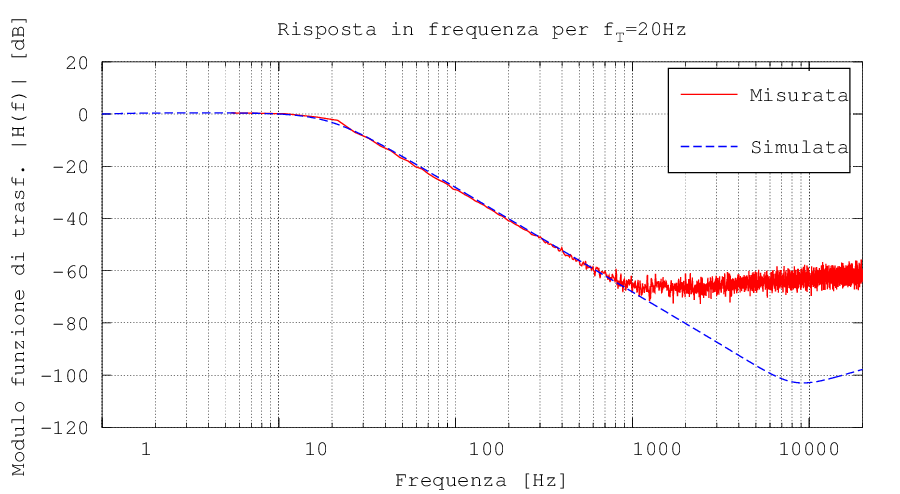Figura 3: Risposta in frequenza del circuito nel caso di frequenza di taglio di 20 Hz. Le curve sono state ottenute mediante simulazione con LTSpice e mediante misura sul circuito reale con una scheda audio del PC e il software Visual Analyser. Lo scostamento tra le due curve alle alte frequenze è dovuto alla scarsa sensibilità e alla rumorosità della scheda audio. In ascissa è riportata la frequenza in coordinate logaritmiche.

Possiamo notare come, nel caso in cui la frequenza di taglio valga 20 Hz, il picco di risonanza sia assente; tale picco compare invece quando f_t = 200 Hz; ciò è coerente con il procedimento di progetto illustrato nella sezione 2, dato che la disequazione che ne garantisce l'assenza è stata valutata in R_P = R_tot, e dunque per f_t = 20 Hz. Il picco di risonanza è tuttavia accettabile.

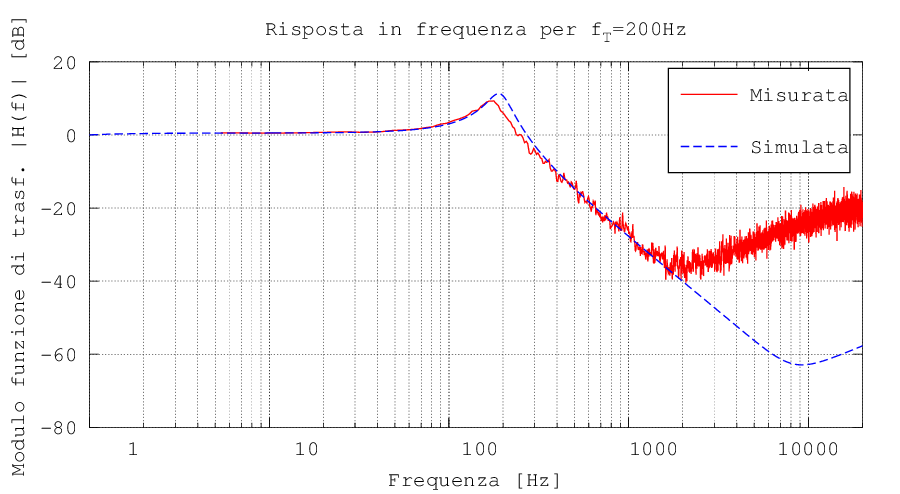Figura 4: Risposta in frequenza del circuito nel caso di frequenza di taglio di 200 Hz. Le curve sono state ottenute mediante simulazione con LTSpice e mediante misura sul circuito reale con una scheda audio del PC e il software Visual Analyser. Lo scostamento tra le due curve alle alte frequenze è dovuto alla scarsa sensibilità e alla rumorosità della scheda audio. In ascissa è riportata la frequenza in coordinate logaritmiche.

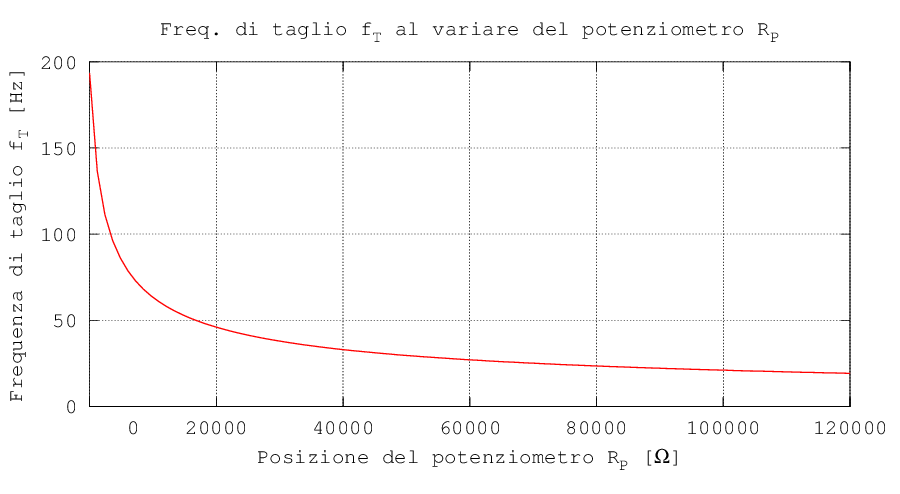
Una nota negativa del filtro è la sensibilità mal distribuita del potenziometro: una variazione lineare della sua resistenza non corrisponde a una variazione lineare della frequenza di taglio. Di seguito, per completezza, è riportata la frequenza di taglio in funzione della resistenza del potenziometro:

Figura 5: Variazione della frequenza in funzione del potenziometro.

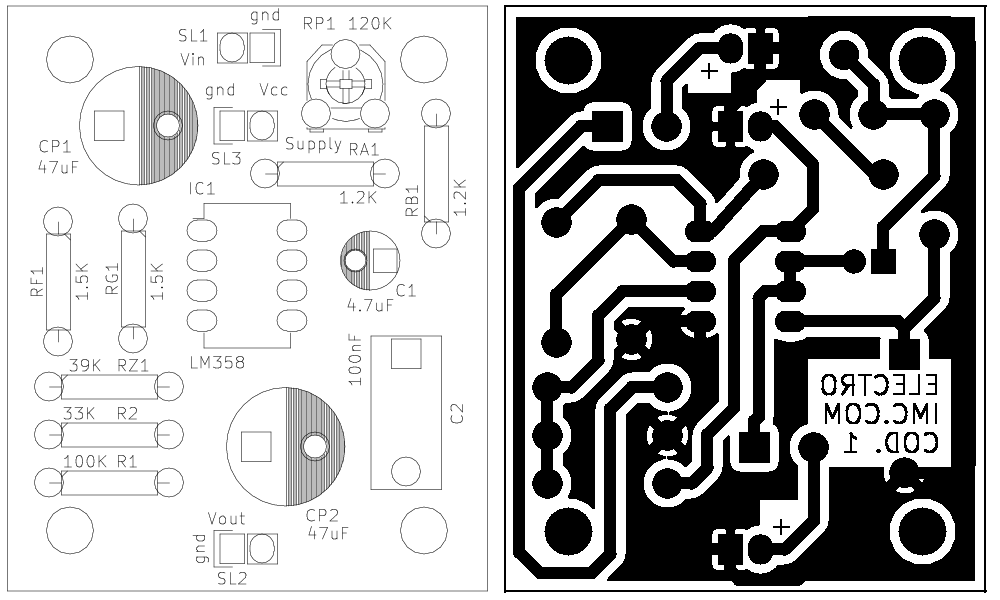
2 - Note costruttive

La realizzazione del circuito non presenta particolari difficoltà, dato che utilizza componenti molto diffusi ed è di dimensioni e complessità ridotte. La scheda mostrata nella figura 1 è di dimensioni 4cm x 5cm, ed è quindi un sottomultiplo dello Standard europeo Eurocard, che prevede schede di dimensioni di 160mm x 100mm. I connettori sono tre: l'ingresso del segnale audio, l'uscita del segnale audio e l'alimentazione.

Scarica il progetto completo in KiCad (68.3Kb)
Scarica lo schema, la scheda elettronica, i file gerber e i pdf per questo progetto.

Figura 6: Serigrafia e circuito stampato del filtro passa basso.

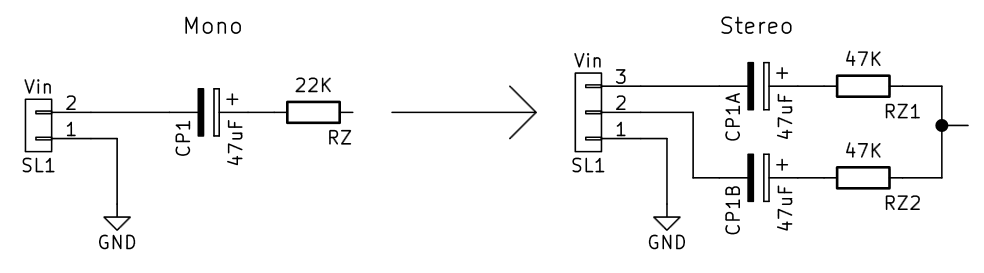
3 - Modifica per ingresso stereo

Il circuito è stato progettato inizialmente per avere un ingresso mono. Le frequenze più basse sono infatti normalmente uguali sul canale destro e sul canale sinistro dei segnali stereo, in quanto il nostro orecchio non ne distingue la provenienza spaziale. Per lo stesso motivo si è soliti avere due casse, una a destra e una a sinistra, per riprodurre le frequenze medie e alte, ma un solo subwoofer in posizione centrale. Viste le richieste nei commenti a questo articolo, vengono proposte due soluzioni:

Collegare all'ingresso del filtro solo il canale sinistro (canale L), dato che i segnali bassi sono uguali su entrambi i canali;
Eseguire la modifica circuitale proposta in Figura 7;

La modifica circuitale prevede che la resistenza di ingresso R_z e il condensatore CP1 non vengano saldati, e al loro posto siano collegate due resistenze con il doppio del valore, insieme al relativo condensatore di disaccoppiamento.

Figura 7: La modifica da apportare all'ingresso del circuito per poter cambiare l'ingresso da mono a stereo. R_z e CP1 devono essere sostituiti da due resistenze in parallelo con il doppio del valore, con i relativi condensatori di disaccoppiamento.

4 - Il progetto: lo stadio di disaccoppiamento e polarizzazione

Il primo stadio del circuito è un amplificatore non invertente, che si occupa di disaccoppiare le tensioni in ingresso al filtro e di polarizzare il segnale sommandovi metà della tensione di alimentazione. Il circuito tradizionale di una amplificatore non invertente prevede che V_IN sia collegata direttamente al piedino non invertente dell'operazionale; in tal caso il guadagno è: 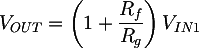$Latex: V_{OUT} = \left(1+\dfrac{R_f}{R_g}\right) V_{IN1}$ In questo caso V_IN è la tensione dopo la rete resistiva formata da R₁, R₂ e R_z. Per calcolare V_IN1 possiamo usare la sovrapposizione degli effetti, seguendo un procedimento analogo a quello utilizzato per dimensionare la polarizzazione dei transistor BJT. 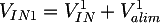La tensione sarà dovuta alla somma di due contributi: la componente V¹_IN dovutoa alla tensione in ingresso V_IN e la componente V¹_alim dovuta alla tensione di alimentazione V_alim: $Latex: V_{IN1} = V^{1}_{IN} + V^{1}_{alim}$

Per determinare il contributo V¹_alim consideriamo il condensatore C_P1 come un circuito aperto, dato che V_alim è una tensione continua: 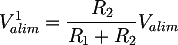$Latex: V^{1}_{alim} = \dfrac{R_2}{R_1+R_2} V_{alim}$ Mentre per determinare il contributo V¹_IN consideriamo V_alim = 0V e quindi sostituiamo all'alimentazione un corto circuito (come vuole il metodo della sovrapposizione degli effetti): 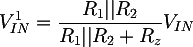$Latex: V_{IN}^{1} = {\dfrac{R_1 || R_2}{R_1 || R_2 + R_z}} V_{IN}$ Unendo i due risultati otteniamo: $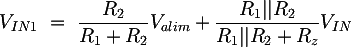Latex: V_{IN1} ~=~ \dfrac{R_2}{R_1+R_2} V_{alim} + \dfrac{R_1 || R_2 }{R_1 || R_2 + R_z} V_{IN}$

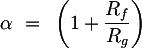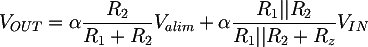
Il guadagno del dell'amplificatore non invertente è indipendente dalle resistenze che compaiono nell'espressione di V_IN1, e quindi possiamo porlo per comodità pari a una costante: $Latex: \alpha~=~\left(1+\dfrac{R_f}{R_g}\right)$ Il guadagno complessivo dello stadio non invertente sarà quindi: $Latex: V_{OUT} = \alpha {\dfrac{R_2}{R_1+R_2}} V_{alim} + \alpha {\dfrac{R_1 || R_2 }{R_1 || R_2 + R_z}} V_{IN}$

4.1 - Scelta dei valori dei componenti

Per determinare i valori dei componenti, possiamo effettuare alcune considerazioni: imponiamo che la tensione V_IN sia riportata uguale all'uscita; per polarizzare correttamente il segnale è necessario che a V_IN sia sommata metà della tensione di alimentazione; infine, scegliamo α = 2, dato che ci permette di utilizzare R_F = R_G. 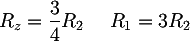Scriviamo quindi un sistema formato dai guadagni di V_IN e V_alim: $Latex: \begin{cases} \alpha\dfrac{R_1 || R_2 }{R_1 || R_2 + R_z} = 1 \\\\[1em] \alpha\dfrac{R_2}{R_1+R_2} = \dfrac{1}{2} \\\\[1em] \alpha=2 \end{cases}$ Da cui otteniamo: $Latex: R_z = \dfrac{3}{4} R_2 ~~~~ R_1 = 3 R_2$ Infine, la resistenza di ingresso del circuito vale: 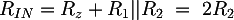$Latex: R_{IN} = R_z + R_1 || R_2 ~=~ 2 R_2$ Scegliendo R₂ = 33 KΩ e tenendo conto delle approssimazioni della serie E12 si ottengono valori ragionevoli: R₁ = 100 KΩ, R_z = 22 KΩ, R_in = 63 KΩ.

4.2 - I condesatori di disaccoppiamento

Il condensatore C_P1 serve a bloccare la corrente di polarizzazione del circuito, in modo che questa non fluisca nel dispositivo collegato all'ingresso. Realizza cioè un filtro passa alto, la cui frequenza di taglio vale: 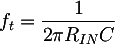$Latex: f_t = \dfrac{1}{2 \pi R_{IN} C}$ Imponiamo che la frequenza di taglio di questo filtro sia molto più piccola della frequenza di lavoro minima del circuito, ad esempio 1Hz. Ricordando che R_in = 66 KΩ, otteniamo C = 2.5 uF. Il condensatore da 47 uF è dunque più che adeguato a garantire il disaccoppiamento. Analoghe considerazioni possono essere fatte per C_P2 sostituendo a R_in la resistenza di carico; tale resistenza sarà altrettanto elevata, dato che corrisponderà all'ingresso di un amplificatore.

5 - Il progetto: il filtro

Lo stadio successivo è il filtro vero e proprio. Per il calcolo della sua funzione di trasferimento esistono numerose dimostrazioni in rete, tra cui quella su Wikipedia in Cella Sallen-Key. Si ottiene: 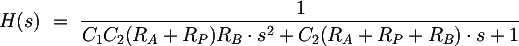$Latex: H(s)~=~\dfrac{1}{ C_1 C_2 (R_A + R_P) R_B \cdot s^2 + C_2 ( R_A+R_P + R_B)\cdot s + 1}$ dove R_P è il valore assunto dal potenziometro P₁. Analizzando questo polinomio è possibile estrarre alcune espressioni matematiche che aiuteranno in fase di progetto.

5.1 - Equazioni di progetto

Se il denominatore ha due poli reali, il diagramma di Bode della funzione di trasferimento inizierà a decrescere in corrispondenza del primo polo con pendenza di -20dB/decade, e poi, in corrispondenza del secondo polo, con pendenza di -40dB/decade. Se invece il denominatore possiede due poli complessi coniugati, vi sarà un'unica frequenza di taglio, in corrispondenza della quale si avrà subito un asintoto con pendenza di -40 dB/decade. E' questa la condizione migliore per il filtro. 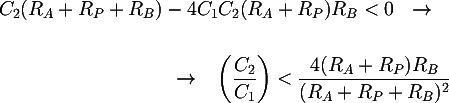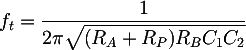Affinchè si verifichi, è necessario che il determinante del denominatore sia negativo: $Latex: C_2 ( R_A+R_P + R_B) - 4 C_1 C_2 (R_A+R_P) R_B < 0 ~~\rightarrow~~ \\\\ ~~\rightarrow~~\left(\dfrac{C_2}{C_1}\right) < \dfrac{ 4 (R_A + R_P)R_B}{(R_A + R_P + R_B)^2}$ In tal caso, la sua frequenza di taglio vale: $Latex: f_t = \dfrac{1}{2 \pi \sqrt{(R_A+R_P) R_B C_1 C_2}}$

Per dimensionare i componenti del filtro, possiamo utilizzare l'espressione della sua frequenza di taglio. Quando il potenziometro è alla fine o all'inizio della corsa si avranno rispettivamente R_P = R_tot, dove R_tot è la resistenza totale del potenziometro, oppure R_P = 0 Ω. In questi due casi si otterranno le frequenze limite f₀ = 20 Hz e f₁ = 200 Hz. 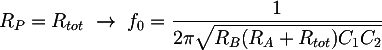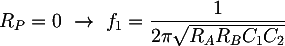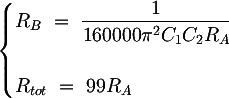La formula della frequenza di taglio si riduce a: $Latex: R_P = R_{tot} ~ \rightarrow ~ f_0 = \dfrac{1}{2 \pi \sqrt{R_B(R_A+R_{tot}) C_1 C_2}}$ $Latex: R_P = 0 ~\rightarrow~ f_1 = \dfrac{1}{2 \pi \sqrt{R_A R_B C_1 C_2}}$ Sostituendo le frequenze limite e risolvendo un sistema contenente le due precedenti equazioni, otteniamo: $Latex: \begin{cases} R_B ~=~ \dfrac{1}{160000 \pi^2 C_1 C_2 R_A} \\\\ {R_{tot} ~=~ 99 R_A}\end{cases}$

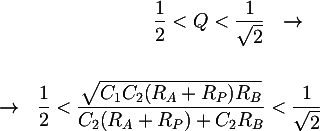
Infine, si può ottenere un'altra condizione di progetto dall'espressione del fattore di qualità. Infatti se la funzione di trasferimento ha poli complessi coniugati, può essere presente un picco di risonanza in corrispondenza della frequenza di taglio. Per eliminare tale picco, il fattore di qualità Q del filtro deve essere limitato: $Latex: \dfrac{1}{2} < Q < \dfrac{1}{\sqrt{2}} ~~ \rightarrow ~~ \\\\ ~~ \rightarrow ~~ \dfrac{1}{2} < \dfrac{\sqrt{C_1C_2(R_A+R_P)R_B}}{C_2(R_A+R_P)+C_2R_B} < \dfrac{1}{\sqrt{2}}$

5.2 - Scelta grafica dei valori dei componenti

Riassumiamo le condizioni imposte finora: $Latex: \begin{cases} R_B ~=~ \dfrac{1}{160000 \pi^2 C_1 C_2 R_A} \\\\[1em] %{R_{tot} ~=~ 99 R_A} \\\\[1em] \left(\dfrac{C_2}{C_1}\right) < \dfrac{ 4 (R_A + R_P)R_B}{(R_A + R_P + R_B)^2} \\\\[1em] %Denominatore comune \dfrac{1}{2} < \dfrac{\sqrt{C_1C_2(R_A+R_P)R_B}}{C_2(R_A+R_P)+C_2R_B} < \dfrac{1}{\sqrt{2}} \\\\[1em] %Fattore qualità \end{cases}$ In ordine, sono l'equazioni ottenuta a partire dalle frequenze di taglio minima e massima, la condizione sul determinante per avere poli complessi coniugati e la condizione sul fattore di qualità per non avere picchi di risonanza.

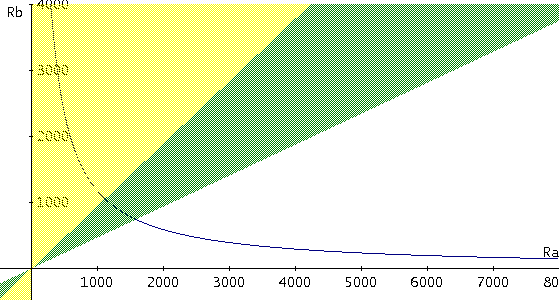
La prima equazione delle tre sopra indicate contiene tutti i componenti di cui calcolare i valori. Per poterli scegliere in maniera rapida e intuitiva la curva è stata disegnata graficamente, ponendo come parametri C₁ e C₂, come variabile indipendente R_A e come variabile dipendente R_B. Sullo stesso grafico sono state colorate di verde e giallo le aree nelle quali è verificata la prima disequazione, relativa al determinante negativo; le aree colorate solo in verde corrispondono invece ai valori per i quali la seconda disequazione, relativa al fattore di qualità limitato, è vera. Le due disequazioni sono valutate supponendo che il potenziometro assuma il suo massimo valore, ovvero che R_P = R_tot = 99R_A. Il grafico, realizzato con Derive 6, è mostrato nella figura seguente, per C₁ = 4.7µF e C₂ = 100nF:

Figura 8: Grafico realizzato in fase di progetto per la scelta dei componenti del filtro.

Impostando i valori parametrici di C₁ e C₂ è possibile tracciare la curva e leggere su di essa i valori di R_A e R_B, mantenendosi all'interno dell'area colorata verde (dove, cioè, sono rispettate entrambe le disequazioni). I valori ottenuti sono così R_A = 1.2 KΩ, R_B = 1.2KΩ, R_tot = 120 KΩ.

Bibliografia e ulteriori letture

Tag