Categorie

Misura della potenza nominale di un trasformatore di alimentazione

Figura 1: Alcuni trasformatori per apparecchi elettronici con dimensioni, uscite e forme differenti.

I trasformatori sono componenti molto comuni e facilmente recuperabili da innumerevoli apparecchi elettronici. Fino a qualche anno fa erano il cuore dell'alimentazione di quasi tutti i dispositivi a bassa tensione, mentre negli ultimi anni sono stati sostituiti dagli alimentatori switching, più leggeri e compatti a parità di potenza. Mentre la misura della tensione di uscita di un trasformatore è un'operazione banale, una stima della sua potenza nominale è un argomento piuttosto complesso. Esistono vari criteri, tutti più o meno rapidi o precisi:

La valutazione a occhio in base alla dimensione del trasformatore, fortemente dipendente dall'esperienza dell'operatore;
Il peso, opportunamente convertito tramite coefficienti;
Formule che considerano la forma, le dimensioni del nucleo, il numero di spire, la sezione dei cavi.

1 - Il principio di misura

A differenza di tutti questi metodi, il sistema di stima presentato in questo articolo si basa sulla misura delle tensioni del trasformatore mentre è in funzione, con carico nullo e sotto carico. Il principale vantaggio è quello di misurare direttamente le grandezze elettriche dalle quali dipende la potenza erogata dal trasformatore, permettendo di raggiungere elevati livelli di precisione.

L'idea fondamentale è la seguente: il trasformatore sta erogando la sua potenza massima quando la tensione di uscita, sotto carico, è un valore compreso tra l'80% e il 90% della sua tensione a vuoto. La percentuale esatta n è un parametro empirico, e varia a seconda dei modelli, ma è comunque possibile ottenere risultati abbastanza precisi.

2 - Il procedimento di misura

Figura 2: Il cicuito di collegamento del trasformatore per effettuare la misura.

Per effettuare la misura, occorre il seguente materiale:

Il trasformatore da misurare;
Un multimetro che permetta di misurare le tensioni alternate (praticamente tutti);
Una resistenza di valore tra i 10 e i 100 Ohm, di elevata potenza (5 W o più, in base al trasformatore);
Spina per collegare il trasformatore alla rete elettrica.

Il procedimento di misura è molto semplice:

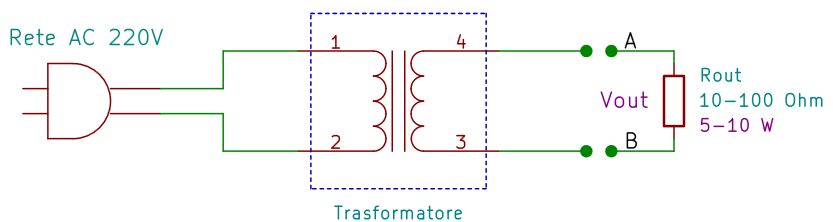
Si misura la tensione d'uscita a vuoto V_s (che, in questo caso, coincide con V_out);
Si collega la resistenza di carico nota all'uscita del trasformatore (ricordiamo che deve avere bassi valori di resistenza, tra i 10 Ω e i 100 Ω, e elevate potenze, 5 W o più);
Si misura la tensione d'uscita V_out ai capi della resistenza (ovvero tra i punti A e B);
Si calcola la potenza del trasformatore con la formula: 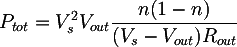$Latex: P_{tot} = V^2_s V_{out} \frac{n(1-n)}{(V_s - V_{out})R_{out}}$ dove:
- V_s è la tensione a vuoto, ovvero senza carico, all'uscita del trasformatore;
- V_out è la tensione misurata ai capi della resistenza di prova;
- R_out è il valore della resistenza di prova;
- n è un valore compreso tra 0.8 e 0.9, tipicamente 0,85.

Eventualmente, è possibile ripetere la misura con più resistenze di carico, in modo da poter tracciare una curva corrente - tensione per verificare la bontà della stima.

3 - La resistenza di carico

La scelta della resistenza di carico è importante per la misura. In teoria qualsiasi valore può essere usato. In pratica, a causa della risoluzione limitata dei comuni multimetri, è opportuno scegliere una resistenza piccola, ad esempio 10 Ω o 100 Ω, in modo da provocare una consistente caduta di tensione all'uscita del trasformatore. Così facendo le incertezze di misura si riducono.

Inoltre, poichè dovrà dissipare molta calore, è opportuno che la resistenza sia di potenza elevata, ad esempio 5 W o più, a seconda del trasformatore; il valore può essere calcolato come: 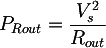$Latex: P_{Rout}= \frac{V_{s}^2}{R_{out}}$ dove

P_Rout è la potenza della resistenza;
V_s è la tensione di uscita del trasformatore a vuoto;
R_out è la resistenza di prova;

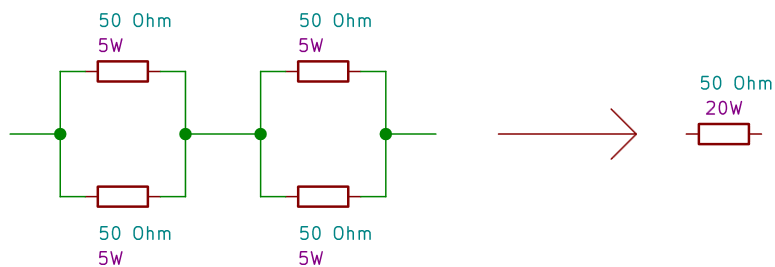
In realtà si possono usare anche resistenze con potenze più basse, a patto che vengano collegate al trasformatore solo per pochi secondi; essendo infatti sottodimensionate, il loro surriscaldamento provoca prima una variazione del loro valore resistivo, e poi la loro rottura. In mancanza di resistenze di potenza adeguata, si possono utilizzare più resistenze in serie o parallelo in modo da distribuire la potenza totale. Un esempio è mostrato nella Figura 3.

Resistenze in serie e parallelo per maggior potenza

Figura 3: Un possibile esempio di come combinare resistenze uguali in serie e in parallelo per ottenre una resistenza dello stesso valore ma maggior potenza.

4 - Il grafico tensione - corrente

Una volta misurata la tensione sul carico R_out è possibile calcolare la corrente erogata dal trasformatore con la legge di Ohm. Se si effettuano più misure con R_out differenti è possibile tracciare un grafico tensione - corrente, che permette di verificare la bontà della stima. In caso di stima corretta, il grafico sarà una retta, che conferma il comportamento ohmico del trasformatore quando non è costretto a erogare una potenza eccessiva. Se la resistenza di carico R_out diventasse molto piccola, cioè se la potenza fornita dal trasformatore fosse molto alta, si verificherebbero vari fenomeni fisici, come la saturazione del nucleo, che renderebbero il comportamento del trasformatore non più lineare; ciò si traduce in una curva tensione - corrente non più retta.

Inoltre nel caso in cui ci sia un errore nella misura (valore di R_out o di V_out errato) la curva mette subito in luce con un dosso o una gobba il valore non corretto.

5 - Esempio: trasformatore 1

Il trasformatore preso in considerazione ha le seguenti caratteristiche:

Tipo: corrente alternata
Tensione da etichetta: 12 V
Tensione misurata a vuoto: 14,2 V
Potenza da etichetta:20 VA

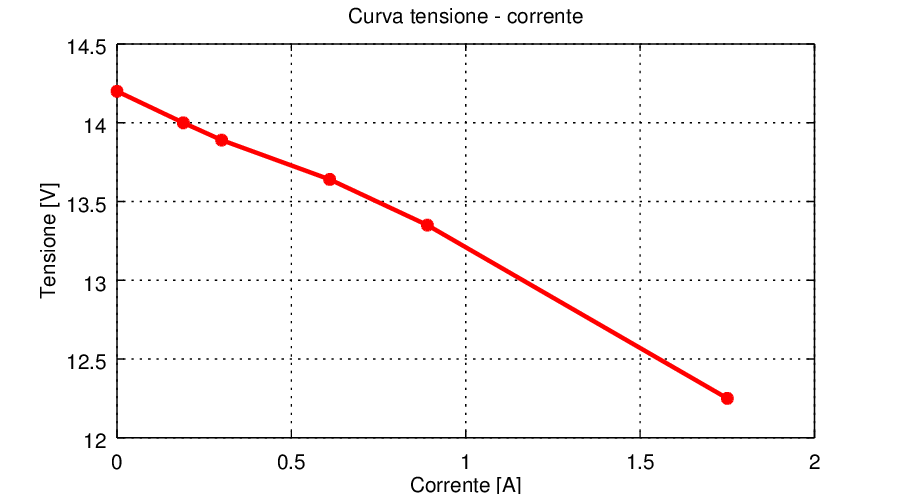
La tabella Tabella 1 mostra varie misure effettuate sul trasformatore con varie resistenze di carico. Ne sarebbe sufficiente solo una per effettuare il calcolo con la Formula 1, ma in questo modo è possibile tracciare il grafico in Figura 5 e verificare che il trasformatore abbia sostanzialmente un comportamento ohmico. Dai valori ottenuti nella tabella è possibile notare come la stima migliore si abbia per un fattore n=0.9, ovvero quando la tensione di uscita è al 90% di quella nominale.

Figura 4: Il trasformatore 1 utilizzato per questo esempio

Tabella 1: trasformatore 1
Tensione sul carico V_out	Resistenza di carico R_out	Corrente nel carico I_out	Potenza per n=0.9 [W]	Potenza per n=0.8 [W]	Resistenza interna R_S
14,2	∞	0
14	73,7	0,19	17,24	30,64	1,05
13,89	46,1	0,30	17,64	31,36	1,03
13,64	22,4	0,61	19,73	35,08	0,92
13,35	15	0,89	19,00	33,78	0,96
12,25	7	1,75	16,29	28,95	1,11
Media:			18	32	1,04

Caratteristica Tensione-Corrente - Trasformatore 1

Figura 5: La caratteristica tensione - corrente del trasformatore, ottenuta effettuando più misure con resistenze di carico diverse. E' una retta, e ciò conferma il comportamento lineare, ovvero ohmico, del trasformatore.

6 - Esempio: trasformatore 2

Il secondo trasformatore di esempio ha le seguenti caratteristiche:

Tipo: corrente alternata
Tensione da etichetta: 14 V
Tensione misurata a vuoto: 15,58 V
Potenza da etichetta: 24 VA

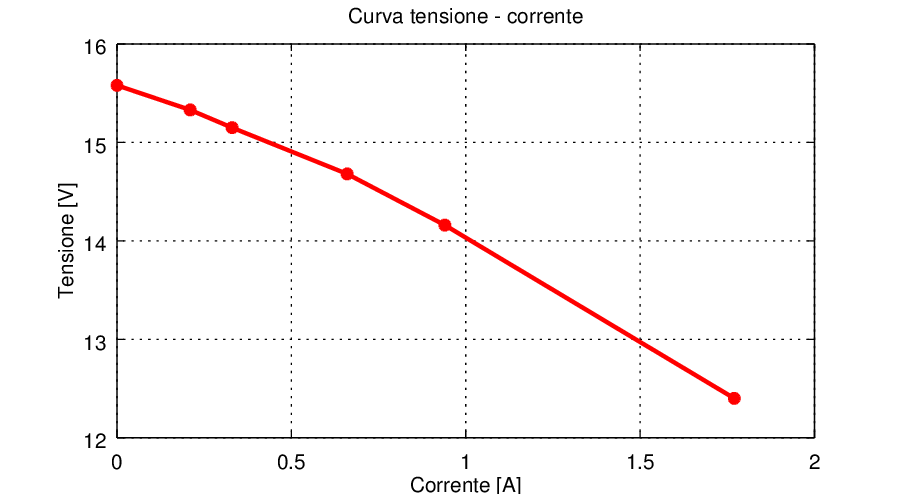
Come per il primo esempio, la Tabella 2 riassume i risultati delle misure effettuate, rappresentati nel grafico della Figura 5. In questo caso la stima migliore si ha per un fattore n=0.8, ovvero quando la tensione di uscita è al 80% di quella nominale.

Figura 6: Il trasformatore 2 utilizzato per questo esempio

Tabella 2: trasformatore 2
Tensione sul carico V_out	Resistenza di carico R_out	Corrente nel carico I_out	Potenza per n=0.9 [W]	Potenza per n=0.8 [W]	Resistenza interna R_S
15,58	∞	0
15,33	73,7	0,21	18,18	32,31	1,20
15,15	46,1	0,33	16,70	29,68	1,31
14,68	22,4	0,66	15,91	28,28	1,37
14,16	15	0,94	14,52	25,82	1,50
12,4	7	1,77	12,17	21,63	1,80
Media:			15	27	1,43

Caratteristica Tensione-Corrente - Trasformatore

Figura 7: Come nel caso del trasformatore 1, la caratteristica tensione - corrente conferma il comportamento lineare e ohmico di questo modello.

7 - Il principio

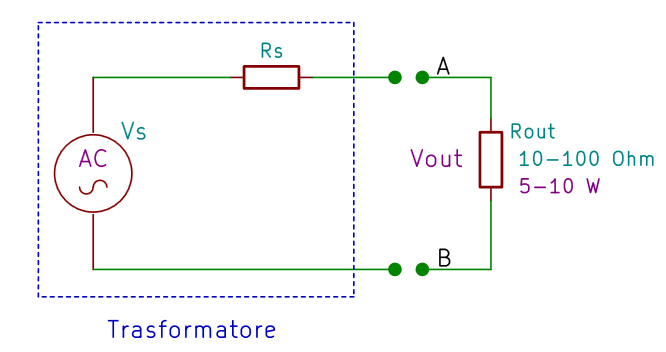
In questa sezione viene illustrata l'origine della formula di calcolo della potenza massima. Esistono vari circuiti equivalenti della porta di uscita di un trasformatore; tra i più semplici, quello che lo paragona a un normale alimentatore con resistenza interna, come mostrato nella Figura 8.

Figura 8: Il circuito equivalente di Thevenin di un trasformatore, modellizzato come elemento puramente lineare.

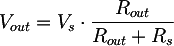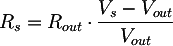
Se inseriamo una resistenza R_out in uscita al trasformatore, creiamo un partitore di tensione. La tensione all'uscita sarà: $Latex: V_{out} = V_{s} \cdot \frac{R_{out}}{R_{out} + R_{s}}$ da cui si ottiene la resistenza interna: $Latex: R_{s} = R_{out} \cdot \frac{V_{s}-V_{out}}{V_{out}}$

Ricordiamo che il principio di misura assume che la potenza massima erogata dal trasformatore si ha quando la sua tensione di uscita è tra l'80% e il 90% della tensione nominale. Definendo il parametro n compreso tra 0.8 e 0.9, la tensione di uscita V_{out n} in corrispondenza della potenza massima vale quindi: $Latex: P_{out} = P_{tot} \rightarrow V_{out n} = n V_{s}$ Possiamo quindi trovare la resistenza R_outn che, collegata al trasformatore, ci permetta di ottenere la tensione V_outn in corrispondenza dell'erogazione della potenza massima; ovvero, calcoliamo il carico che fa erogare al trasformatore la massima potenza. Dal partitore precedentemente scritto si ha: 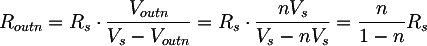$Latex: R_{out n} = R_{s} \cdot \frac{V_{out n}}{V_{s}-V_{out n}} = R_{s} \cdot \frac{nV_{s}} {V_{s}-nV_{s}} = \frac{n}{1-n}R_{s}$ La potenza con V_{out n} e R_{out n} sarà quindi: 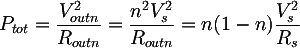$Latex: P_{tot} = \frac{V^2_{out n}}{R_{out n}} = \frac{n^2 V^2_{s}}{R_{out n}} = n(1-n) \frac{V_{s}^{2}}{R_{s}}$ Da cui, sostituendo l'espressione di R_s prima trovata, si ottiene la formula finale: $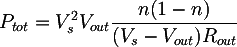Latex: P_{tot} = V^2_s V_{out} \frac{n(1-n)}{(V_s - V_{out})R_{out}}$

Tag